2017高考数学首轮考点训练-选考内容含答案解析
第十三章 选考内容
考纲链接
1.几何证明选讲
(1)理解相似三角形的定义与性质,了解平行截割定理.
(2)会证明和应用以下定理:
①直角三角形射影定理;
②圆周角定理;
③圆的切线判定定理与性质定理;
④相交弦定理;
⑤圆内接四边形的性质定理与判定定理;
⑥切割线定理.
2.坐标系与参数方程
(1)了解坐标系的作用,了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.
(2)了解极坐标的基本概念,会在极坐标系中用极坐标刻画点的位置,能进行极坐标和直角坐标的互化.
(3)能在极坐标系中给出简单图形表示的极坐标方程.
(4)了解参数方程,了解参数的意义.
(5)能选择适当的参数写出直线、圆和椭圆的参数方程.
3.不等式选讲
(1)理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:
①|a+b|≤|a|+|b|(a,b∈R);
②|a-b|≤|a-c|+|c-b|(a,b∈R).
(2)会利用绝对值的几何意义求解以下类型的不等式:
|ax+b|≤c; |ax+b|≥c; |x-c|+|x-b|≥a.
(3)通过一些简单问题了解证明不等式的基本方法:比较法、综合法、分析法.
§13.1 几何证明选讲
1.平行线等分线段定理
如果一组平行线在一条直线上截得的线段相等,那么在其他直线上截得的线段____________.
推论1:经过三角形一边的中点与另一边平行的直线必____________.
推论2:经过梯形一腰的中点,且与底边平行的直线____________.
2.平行线分线段成比例定理
三条平行线截两条直线,所得的对应线段________.
推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段________.
3.相似三角形的判定定理
判定定理1:对于任意两个三角形,如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.简述为:两角对应________,两三角形相似.
判定定理2:对于任意两个三角形,如果一个三角形的两边和另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似.简述为:两边对应成________且夹角________,两三角形相似.
判定定理3:对于任意两个三角形,如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形相似.简述为:三边对应________,两三角形相似.
注意:与一般三角形相比,直角三角形有一个角为直角,三边长满足勾股定理等.这种关系可以使判定两个直角三角形相似的条件得到简化.
4.相似三角形的性质定理
性质定理1:相似三角形对应高的比、对应中线的比和对应角平分线的比都等于____________.
性质定理2:相似三角形周长的比、外接圆的直径比、外接圆的周长比都等于____________.
性质定理3:相似三角形面积的比、外接圆的面积比都等于____________.
5.射影定理
直角三角形斜边上的高是______________________的比例中项;两直角边分别是它们在斜边上射影与斜边的_________________________.
6.圆周角、圆心角和弦切角定理
①圆周角定理:圆上一条弧所对的圆周角等于它所对的____________的一半.
②圆心角定理:圆心角的度数等于它所对______的度数.
推论1:同弧或等弧所对的圆周角________;同圆或等圆中,相等的圆周角所对的弧____________.
推论2:半圆(或直径)所对的圆周角是________;90°的圆周角所对的弦是________.
③弦切角定理:弦切角等于它所夹的弧所对的________.
7.圆内接四边形的性质与判定定理
(1)性质定理:圆的内接四边形的对角____________.
推论:圆内接四边形的外角等于它的__________的对角.
(2)判定定理:如果一个四边形的对角互补,那么这个四边形的四个顶点____________.
推论:如果四边形的一个外角等于它的内角的对角,那么这个四边形的四个顶点____________.
8.圆的切线的性质与判定定理
性质定理:圆的切线垂直于经过切点的________.
推论1:经过圆心且垂直于切线的直线必经过________.
推论2:经过切点且垂直于切线的直线必经过________.
判定定理:经过半径的外端并且垂直于这条半径的直线是圆的________.
9.相交弦定理
圆内的两条相交弦,________________________的积相等.
10.(1)割线定理:从圆外一点引圆的两条割线,这一点到__________________的两条线段长的积相等.
(2)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到______________________________的比例中项.
(3)切线长定理:从圆外一点引圆的两条切线,它们的切线长________,圆心和这一点的连线平分____________的夹角.且____________切点弦.
自查自纠:
1.也相等 平分第三边 平分另一腰
2.成比例 成比例
3.相等 比例 相等 成比例
4.相似比 相似比 相似比的平方
5.两直角边在斜边上射影 比例中项
6.①圆心角 ②弧 相等 也相等 直角 直径 ③圆周角
7.(1)互补 内角 (2)共圆 共圆
8.半径 切点 圆心 切线
9.被交点分成的两条线段长
10.(1)每条割线与圆的交点
(2)割线与圆交点的两条线段长
(3)相等 两条切线 垂直平分
如图, 在△ABC中,AE=ED=DC,FE∥MD∥BC,FD的延长线交BC的延长线于点N,且EF=1,则BN=( )
A.2 B.3
C.4 D.6
解:∵FE∥MD∥BC,AE=ED=DC,
∴EFBC=AEAC=13,EFCN=EDDC=1,
∴EF=CN,∴EFBN=EFBC+CN=14,
∴BN=4EF=4.故选C.
如图AD是△ABC的中线,E是CA边靠近C点的三等分点,BE交AD于点F,则AF∶FD为( )
A.2∶1 B.3∶1
C.4∶1 D.5∶1
解:过D作DG∥AC交BE于G,则DG=12EC,又AE=2EC,△DGF∽△AEF,
故AF∶FD=AE∶DG=2EC∶12EC=4∶1.故选C.
如图,∠ACB=90°,CD⊥AB于点D,以BD为直径的圆与BC交于点E.则( )
A.CECB=ADDB
B.CECB=ADAB
C.ADAB=CD2
D.CEEB=CD2
解:在△ACB中,因为∠ACB=90°,CD⊥AB于点D,所以CD2=ADDB.又由切割线定理得CD2=CECB,所以CECB=ADDB.故选A.
如图,过点D作圆的切线切圆于B点,作割线交圆于A,C两点,其中BD=3,AD=4,AB=2,则BC=________.
解:由切割线定理得:BD2=CDAD,得CD=94.
又∵∠A=∠DBC,∠D=∠D,
∴△ABD∽△BCD,BDCD=ABBC,解得BC=32.故填32.
(2015重庆)如图,圆O的弦AB,CD相交于点E,过点A作圆O的切线与DC的延长线交于点P,若PA=6,AE=9,PC=3,CE∶ED=2∶1,则BE=____________.
解:由切割线定理,知PA2=PC倠D,即62=3PD,解得PD=12,∴CD=PD-PC=9,∴CE=6,ED=3.由相交弦定理,知AEBE=CEED,即9BE=6×3,解得BE=2.故填2.
类型一 平行线分线段成比例定理的应用
如图,在△ABC中,EF∥CD,∠AFE=∠B,AE=6,ED=3,AF=8.
(1)求AC的长;
(2)求CD2BC2的值.
解:(1)∵EF∥CD,∴AEAD=AFAC.
∵AE=6,ED=3,AF=8,∴66+3=8AC,
∴AC=12.
(2)∵EF∥DC,∴∠AFE=∠ACD,
又∠AFE=∠B,∴∠ACD=∠B.
又∠A=∠A,∴△ACD∽△ABC.
∴CDBC=ADAC=6+312=34,∴CD2BC2=916.
点拨:
求长度或比值考虑相似,有时图形中没有平行线,要添加辅助线,构造相关图形,即创造可以形成比例式的条件,从而达到计算或证明的目的.
(1)如图所示,在△ABC中,D是BC的中点,E是AC的中点,AD交BE于G,求证:AG=2GD.
证明:作CH∥EB交AD的延长线于点H,
∵AE=EC,CH∥EB,∴AG=GH.
又∵BD=DC,
∴△BDG≌△CDH.
∴GD=DH.∴AG=2GD.
(2)在△ABC中,AD为∠BAC的平分线,求证:ABAC=BDDC.
证明:如图,过C作CE∥AD,交BA延长线于E,
∵AD∥CE,∴BAAE=BDDC.
∵AD平分∠BAC,
∴∠BAD=∠DAC.
由AD∥CE知∠BAD=∠E,
∠DAC=∠ACE,
∴∠ACE=∠E,即AE=AC.
∴ABAC=BDDC .
类型二 相似三角形的判定及性质
如图所示,已知在△ABC中,∠BAC=90°,AD⊥BC,E是AC的中点,ED交AB的延长线于F,求证:ABAC=DFAF.
证明:∵∠BAC=90°,AD⊥BC,
∴△ABD∽△CAD,
∴ABAC=BDAD.①
又∵E是AC的中点,∴DE=EC,
∴∠4=∠3=∠ACB=∠1,而∠AFD为公共角,
∴△FBD∽△FDA,
∴BDAD=DFAF,②,由①②可得ABAC=DFAF.
点拨:
(1)判定两个三角形相似要注意结合图形性质灵活选择判定定理,特别要注意对应角和对应边.(2)相似三角形的性质可用来证明线段成比例、角相等,也可用来间接证明线段相等或计算线段长度.
(2014中原名校联考)如图, 三角形ABC的角平分线AD的延长线交它的外接圆于点E.
(1)证明:△ABE∽△ADC;
(2)若三角形ABC的面积S=12ADAE,求∠BAC的大小.
解:(1)证明:由已知条件,可得∠BAE=∠CAD,因为∠AEB与∠ACB是同弧所对的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(2)因为△ABE∽△ADC,所以ABAD=AEAC, ※
又S=12ABAC猠椀渀∠BAC且S=12ADAE,故ABAC猠椀渀∠BAC=ADAE,由※可知ABAC=ADAE,则sin∠BAC=1,又∠BAC为△ABC的内角,所以∠BAC=90°.
类型三 射影定理的应用
如图所示,已知在边长为1的正方形ABCD的一边上取一点E,使AE=14AD,过AB的中点F作HF⊥EC于H.
(1)求证:FH=FA;
(2)求EH∶HC的值.
解:(1)证明:连结EF,FC,在正方形ABCD中,
AD=AB=BC,∠A=∠B=90°.
∵AE=14AD,F为AB的中点,
∴AEAF=FBBC =12.
∴△EAF∽△FBC.
∴∠AEF=∠BFC,∠EFA=∠BCF.
又∠A=∠B=90°,∴∠EFC=90°,EFFC=AEBF=AEAF=12.
又∵∠EFC=∠A=90°,∴△EFC∽△EAF.
∴∠AEF=∠HEF.
又EF=EF,
∴Rt△EAF≌Rt△EHF.∴FH=FA.
(2)由(1)知△EFC是直角三角形,FH是斜边EC上的高,
由射影定理可得EF2=EHEC,FC2=CHCE,于是EH∶HC=EF2∶FC2=1∶4.
点拨:
①一般四边形问题须转化为三角形(最好是Rt△)问题研究,故自然要连结EF,FC,第(1)问也可由勾股定理求出FH的长来证;②图中有2对全等三角形,8对相似三角形,能洞察这些,解此题会游刃有余;③第(2)问由EH∶HC=AE∶BC求,更简洁.
如图所示,AD,BE是△ABC的两条高,DF⊥AB,垂足为F,直线FD交BE于点G,交AC的延长线于H,求证:DF2=GFHF.
证明:∵∠H+∠BAC=90°,
∠GBF+∠BAC=90°,∴∠H=∠GBF.
∵∠AFH=∠GFB=90°,
∴△AFH∽△GFB,∴HFBF=AFGF,
∴AFBF=GFHF.
因为在Rt△ABD中,FD⊥AB,∴DF2=AFBF,
∴DF2=GFHF.
类型四 圆内接四边形的性质及判定定理的应用
(2015哈三中一模)如图,AB是⊙O的直径,CB与⊙O相切于B,E为线段CB上一点,连接AC,AE,分别交⊙O于D,G两点,连接DG并延长交CB于点F.
(1)求证:C,D,G,E四点共圆;
(2)若F为EB的靠近点E的三等分点,EG=1,GA=3,求线段CE的长.
解:(1)证明:连接BD,则∠AGD=∠ABD,∠ABD+∠DAB=90°,∠C+∠CAB=90°,所以∠C=∠AGD,所以∠C+∠DGE=180°,所以C,D,G,E四点共圆.
(2)因为EGEA=EB2,所以EB=2,又F为EB的三等分点,所以EF=23,FB=43,
又因为FGFD=FEFC=FB2,所以FC=83,CE=2.
点拨:
①直径所对圆周角为直角,故考虑连BD;②证明四点共圆,即证明这四点构成的四边形对角互补;③已知条件为EG及GA的长度,自然考虑计算EB,从而求得FGFD,再计算EC即可.
(2014新课标Ⅰ)如图,四边形ABCD是⊙O的内接四边形,AB的延长线与DC的延长线交于点E,且CB=CE.
(1)证明:∠D=∠E;
(2)设AD不是⊙O的直径,AD的中点为M,且MB=MC,证明:△ADE为等边三角形.
证明:(1)由题设知A,B,C,D四点共圆,所以∠D=∠CBE,由已知CB=CE得∠CBE=∠E,故∠D=∠E.
(2)如图,设BC的中点为N,连结MN,则由MB=MC知MN⊥BC,故O在直线MN上.
又AD不是⊙O的直径,M为AD的中点,故OM⊥AD,即MN⊥AD.
所以AD∥BC,故∠A=∠CBE.
又∠CBE=∠E,故∠A=∠E,由(1)知,∠D=∠E,
所以△ADE为等边三角形.
类型五 圆的切线及与圆有关的比例线段
(2015唠羖)如图,AB切⊙O于点B,直线AO交⊙O于D,E两点,BC⊥DE,垂足为C.
(1)证明:∠CBD=∠DBA;
(2)若AD=3DC,BC=2,求⊙O的直径.
解:(1)证明:∵DE为⊙O的直径,则∠BED+∠EDB=90°,
又BC⊥DE,∴∠CBD+∠EDB=90°,
从而∠CBD=∠BED.
又AB切⊙O于点B,得∠DBA=∠BED,
∴∠CBD=∠DBA.
(2)由(1)知BD平分∠CBA,
则BABC=ADCD=3,又BC=2,从而AB=32,
∴AC=AB2-BC2=4,∴AD=3.
由切割线定理得AB2=ADAE,即AE=AB2AD=6,
故DE=AE-AD=3,即⊙O的直径为3.
点拨:
①与切线有关的角的证明问题,一般都要用到弦切角定理;②计算与圆相关的线段长度问题,一般都要用到圆幂定理;③注意三角形内角平分线定理的灵活应用.
(2015吉林长春调研)如图,圆M与圆N交于A,B两点,以A为切点作两圆的切线分别交圆M和圆N于C,D两点,延长DB交圆M于点E,延长CB交圆N于点F.已知BC=5,BD=10.
(1)求AB的长;(2)求CFDE.
解:(1)根据弦切角定理,
知∠BAC=∠BDA,∠ACB=∠DAB,
∴△ABC∽△DBA,则ABDB=BCBA,
故AB2=BCBD=50,AB=52.
(2)根据切割线定理,知CA2=CBCF,DA2=DBDE,
两式相除,得CA2DA2=CBDBCFDE,*
由△ABC∽△DBA,得ACDA=ABDB=5210=22,CA2DA2=12,
又CBDB=510=12,由*得CFDE=1.
1.用添加平行辅助线的方法构造平行线,是创造应用平行线等分线段定理与平行线分线段成比例定理的条件.在使用平行线分线段成比例定理及推论时,一定要注意线段与边的对应.
2.在证明两个或两个以上的比例式相等时,往往需要找第三个比例式与它们都相等,这时可考虑利用平行线分线段成比例定理或推论,或考虑用线段代换,由相等的传递性得出结论.
3.证两个三角形相似,在已具备一角对应相等的条件时,往往先探求是否有另一角对应相等,当此思路不通时,再探求等角的两边对应成比例.
4.等积式的证明是一种常见题型,其证题思路一般是化等积式为比例式,再由三角形相似或平行线分线段成比例定理证明.
5.注意在证明圆的有关问题时,常常需要添加辅助线,添加辅助线的目的是为了打通已知与未知的通道,构造需要的边、角、三角形,如构造直径所对的圆周角,以便利用直径所对的圆周角是直角这一性质.要证明某直线是圆的切线,如果已知直线过圆上某一点,那么连接这点和圆心,证明该直线垂直于半径;如果不知直线和圆是否有公共点,则过圆心作直线的垂线,证明圆心到直线的距离等于半径.已知某直线是圆的切线时,切点的位置一般是确定的,辅助线常常是连接圆心和切点.
6.证明多点共圆的常用方法
(1)证明几个点到某个定点距离相等;
(2)如果某两点在某条线段的同旁,证明这两点对这条线段的张角相等(例:如图,若∠ACB=∠ADB=90°,则A,B,D,C四点共圆).
(3)证明凸四边形内对角互补(或外角等于它的内角的对角).
7.相交弦定理、切割线定理和割线定理常与圆周角、弦切角定理联合运用,要注意在题中找相等的角,找相似三角形,从而得到线段的比或比例式.
1.如图,在△ABC中,∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )
A.154 B.7 C.152 D.245
解:由已知条件∠AED=∠B,∠A为公共角,所以△ADE∽△ACB,则有DEBC=AEAB,从而BC=6×108=152.故选C.
2.如图,半径为2的⊙O中,∠AOB=90°,D为OB的中点,AD的延长线交⊙O于点E,则线段DE的长为( )
A.52 B.255 C.355 D.32
解:延长BO交⊙O于点F,由相交弦定理可知:BDDF=ADDE.又由题知BD=1,DF=3,AD=5,因此DE=355.故选C.
3.如图,⊙O与⊙P相交于A,B两点,点P在⊙O上,⊙O的弦BC切⊙P于点B,CP及其延长线交⊙P于D,E两点,过点E作EF⊥CE交CB延长线于点F.若CD=2,CB=22,则EF的长为( )
A.1 B.2 C.2 D.22
解:连结PB,BC切⊙P于点B,PB⊥BC,CD=2,CB=22,由切割线定理得CB2=CDCE,CE=4,DE=2,BP=1,又∵EF⊥CE,∴△CPB∽△CFE,得EFPB=CECB,解得EF=2.故选B.
4.如图,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.
给出下列三个结论:
①AD+AE=AB+BC+CA;
②AFAG=ADAE;
③△AFB∽△ADG.
其中正确结论的序号是( )
A.①② B.②③ C.①③ D.①②③
解:∵CF=CE,BF=BD,∴BC=CE+BD.
∴AB+BC+CA=(AB+BD)+(AC+CE)=AD+AE.故结论①正确.
由切割线定理知AD2=AFAG,又AE=AD,∴ADAE=AFAG,故结论②正确.容易判断结论③不正确.故选A.
5.(2015天津)如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N.若CM=2,MD=4,CN=3,则线段NE的长为( )
A.83 B.3 C.103 D.53
解:由题意可得CM×MD=AM×MB=AN×NB=CN×NE,即2×4=3NE,解得NE=83.故选A.
6.(2014天津)如图,△ABC是圆的内接三角形,∠BAC的平分线交圆于点D,交BC于点E,过点B的圆的切线与AD的延长线交于点F.在上述条件下,
给出下列四个结论:
①BD平分∠CBF; ②FB2=FDFA;
③AECE=BEDE; ④AFBD=ABBF.
则所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②④
解:由弦切角定理得∠FBD=∠EAC=∠BAE,又∠BFD=∠AFB,故△BFD∽△AFB,故BFAF=BDAB,即AFBD=ABBF,④对,否定A,C.显然②正确.故选D.
7.(2014重庆)过圆外一点P作圆的切线PA(A为切点),再作割线PBC依次分别交圆于B,C,若PA=6,AC=8,BC=9,则AB=__________.
解:如图,
由PA2=PB倠C得62=PB(PB+9),解得PB=3.再由∠C=∠BAP及∠P为公共角得△ABP∽△CAP,∴ABCA=BPAP,∴AB=4.故填4.
8.(2015缠东)如图,已知AB是圆O的直径,AB=4,EC是圆O的切线,切点为C,BC=1,过圆心O作BC的平行线,分别交EC和AC于点D和点P,则OD=__________.
解:由题意得OP=12BC=12,OA=2,于是PA=CP=22-122=152,由于∠DCP=∠B=∠POA△DCP∽△AOP,于是PDPA=PCPO倡D=15212×152=152,那么OD=152+12=8.故填8.
9.(2015嘠坮)如图,在⊙O中,相交于点E的两弦AB,CD的中点分别是M,N,直线MO与直线CD相交于点F.证明:
(1)∠MEN+∠NOM=180°;
(2)FEFN=FMFO.
证明:(1)如图所示,∵M,N分别是弦AB,CD的中点,∴OM⊥AB,ON⊥CD,即∠OME=∠ENO=90°,故∠MEN+∠NOM=180°.
(2)由(1)知,O,M,E,N四点共圆,故由割线定理即得FEFN=FMFO.
10.如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=20,PB=10,∠BAC的角平分线与BC和圆O分别交于点D和E.
(1)求证:AB倠C=PAAC;
(2)求ADAE的值.
解:(1)证明:∵PA为圆O的切线,
∴∠PAB=∠ACP,又∠P为公共角,
∴△PAB∽△PCA,∴ABAC=PAPC,∴AB倠C=PAAC.
(2)∵PA为圆O的切线,PC是过点O的割线,
∴PA2=PB倠C,∴PC=40,BC=30,
又∵∠CAB=90°,∴AC2+AB2=BC2=900,
又由(1)知ABAC=PAPC=12,∴AC=125,AB=65,连接EC,则∠CAE=∠EAB,△ACE∽△ADB,ABAE=ADAC,ADAE=ABAC=65×125=360.
11.(2014新课标Ⅱ)如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E.证明:
(1)BE=EC;(2)ADDE=2PB2.
证明:(1)连接AB,AC.由题设知PA=PD,故∠PAD=∠PDA.
∵∠PDA=∠DAC+∠DCA,
∠PAD=∠BAD+∠PAB,∠DCA=∠PAB,
∴∠DAC=∠BAD,从而BE︵=EC︵.
因此BE=EC.
(2)由切割线定理得PA2=PB倠C.
∵PA=PD=DC,∴DC=2PB,BD=PB.
由相交弦定理得ADDE=BDDC,
∴ADDE=PB㈠倀B=2PB2.
(2015栠国Ⅱ)如图,O为等腰三角形ABC内一点,⊙O与△ABC的底边BC交于M,N两点,与底边上的高AD交于点G,且与AB,AC分别相切于E,F两点.
(1)证明:EF∥BC;
(2)若AG等于⊙O的半径,且AE=MN=23,求四边形EBCF的面积.
解:(1)证明:由于△ABC是等腰三角形,AD⊥BC,∴AD是∠CAB的平分线.
又∵⊙O分别与AB,AC相切于点E,F,∴AE=AF,故AD⊥EF.从而EF∥BC.
(2)由(1)知,AE=AF,AD⊥EF,故AD是EF的垂直平分线.又EF为⊙O的弦,∴O在AD上.
连接OE,OM,则OE⊥AE.
由AG等于⊙O的半径得AO=2OE,∴∠OAE=30°.因此△ABC和△AEF都是等边三角形.
∵AE=23,∴AO=4,OE=2.
∵OM=OE=2,DM=12MN=3,∴OD=1.
于是AD=5,AB=1033.
∴四边形EBCF的面积为
12×10332×32-12×(23)2×32=1633.
Tags:极坐标 不等式 坐标系 绝对值 三角形 平行线 圆周角 射影 综合法
相关文章
-
2023-10-16

高考数学星老师:寻找相似之处
我是高考数学星老师,努力耕耘的高中数学教师一名,喜欢分享自己的教学心得和教学成果,比较关注现代教育圈话题,既热衷于研究中学阶段学生学习方法,亦致力于培养青春期学生的良好心理素质。如果您是家长或者教育工作者,和我一样志同道合,欢迎您关注、点赞、转发、收藏,一起为教育事业尽力!有..
-
2020-10-12

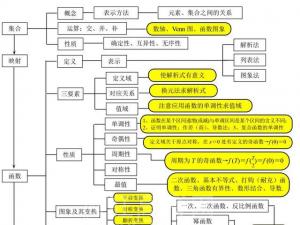
清华学霸坦言:高中数学只要吃透这6张图,3年数学不下140!
想要在数学的学习上取得好成绩,无非就要掌握好6个字“,多总结、多反思”。盲目的题海战术往往都是事倍功半!效率是极低的!你刷的很多题目都是没用的,甚至高考根本不可能考查。但并不否认题海战术的重要性,在中学阶段,合理的利用题海战术可以帮助学生总结归纳答题步骤和规律,醉倒举一反三,下..
-
2020-08-29

中数学成绩老是上不去?北大状元学习方法送给你!
这篇文章,我要终结关于高中数学学习方法的讨论。说要终结高中数学学习方法的讨论,是开玩笑,但的确是我这些年对于高中数学学习方法的经验的总结,也受到知乎很多答主的启发。所以发在这里,希望能回馈更多的高中生,对同学们有用。一、关于高中数学你需要了解一些什么?高中数学就是先让你学一些..
猜你喜欢
-
2019-11-16

准高三生们:物理一轮复习方法与策略
用对的学习方法和学习技巧来学习,成绩自然就会提高,还好,有清华北大的伙伴们编写的《疯狂600提分笔记》解读高考出题规律,答题技巧,应试技巧等。高考是高中阶段学习的指挥棒,高考怎么考、高校怎么招生牵动着全国家长和考生的注意力。上海和浙江两地区是新高考政策的试点地区,率先进行高考改革..
-
2019-04-21
不知道该选择谁
1、有个人生病了,他找一位医生看病,医生给他看完病开药时说:“大的一天吃两片,小的一天吃一片。”他回到家里,对两个孩子说:“老大,这大药片你一天吃两片;老二:这小片的你一天吃一片。”2、姑娘问她的闺蜜:“我认识了两个男孩,不知道该选择谁。”闺蜜问:“那他们是做什么的?”姑娘:“..
-
2020-10-20
高三生物复习要点:新陈代谢
机体与外界环境之间的物质和能量交换以及生物体内物质和能量的自我更新过程叫做新陈代谢。新陈代谢包括合成代谢(同化作用)和分解代谢(异化作用)。肠道是人体最大的消化器官,益生菌参与人体的消化、吸收与排泄。下面是小编整理的高三生物复习要点:新陈代谢,高三同学们可以参考借鉴。1、新陈代谢是..
-
2019-10-15
平面解析几何是数形结合的典范,是高中数学的主要知识模块
用对的学习方法和学习技巧来学习,成绩自然就会提高,还好,有清华北大的伙伴们编写的《疯狂600提分笔记》解读高考出题规律,答题技巧,应试技巧等。平面解析几何是数形结合的典范,是高中数学的主要知识模块,是高考考查的重点和难点,也是联系初等数学与高等数学的纽带,它侧重于形象思维、推理运..
-
2019-04-15
你测测我的蚊帐是谁偷的
1、有个妇人刚买的蚊帐被偷了,心里很是郁闷,便找街上的一位测字算命的问问是谁偷的。她到了那里说:“先生,我要测字。”算命先生:“你要测什么事呀?”妇人:“你测测我的蚊帐是谁偷的”测字先生想:我也不是警察,谁知道你的蚊帐是谁偷的,不过有钱不赚是傻瓜.“那你就写个吧。”妇人不认字.但会..